Depth First Search (DFS)

965

DFS (Depth First Search) is a technique used for traversing trees or graphs. In this traversal first, the deepest node is visited and then backtracks to its parent node if no sibling of that node exists.

DFS is commonly used to solve various graph-related problems, such as finding connected components, topological sorting, and solving mazes.

Concept of Depth First Search

Step 1: Traverse the root node.

Step 2: Traverse any neighbour of the root node.

Step 3: Traverse any neighbour of neighbour of the root node.

Step 4: This process will continue until we are getting the goal node.

Examples

Example 1:
Input:

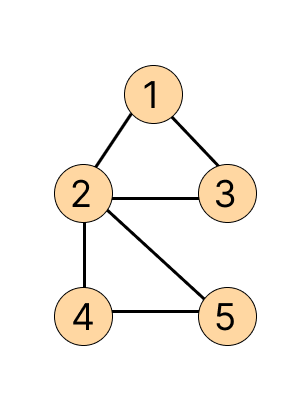
Output: 1 2 4 5 3

Example 2:
Input:

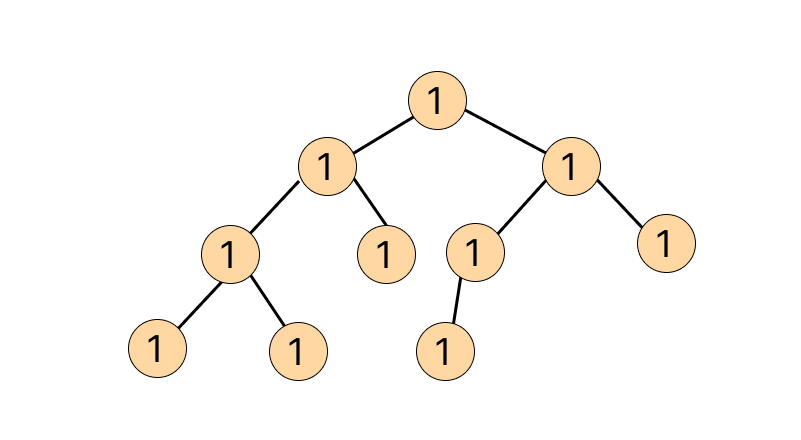
Output: 1 2 3 4 5 6 7 8 9 10

Algorithm of DFS

Step 1: PUSH the starting node into the stack.

Step 2: If the stack is empty then stop and return failure.

Step 3: If the top node of the stack is the goal node, then stop and return success.

Step 4: Else POP the top node from the stack and process it. Find all its neighbours that are in ready stateand PUSH them into the stack in any order.

Step 5: Go to step 3.

Step 6: Exit

Advantages of DFS

1. DFS consumes very less memory space.
2. It will reach at the goal node in a less time period than BFS if it traverses in a right path.
3. It may find a solution without examining much of search because we may get the desired solution in the very first go.

Disadvantages of DFS

1. It is possible that may states keep reoccurring.
2. There is no guarantee of finding the goal node.
3. Sometimes the states may also enter into infinite loops.

Application of DFS Algorithm

1. For finding the path
2. To test if the graph is bipartite
3. For finding the strongly connected components of a graph
4. For detecting cycles in a graph